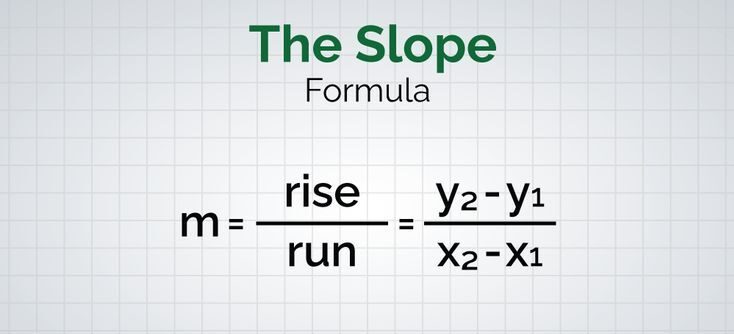Understanding how to calculate the slope of a line is essential in various fields, including mathematics, physics, and engineering. The slope represents the steepness or incline of a line and is a crucial concept in algebra and calculus. This guide will walk you through the basic things you need to know about slopes, followed by detailed methods on how to find the slope and the different types of slopes you might encounter.
Things You Should Know
Before diving into the methods, here are a few fundamental concepts you should understand about the slope of a line:
- Definition of Slope: The slope (often denoted as “m”) measures the rate at which the y-coordinate of a point on the line changes as the x-coordinate changes. It is calculated as the ratio of the vertical change (rise) to the horizontal change (run) between two points on the line.
- Slope Formula: The slope between two points ((x1, y1)) and ((x2, y2)) on a line is given by the formula:
[m = \frac{y2 – y1}{x2 – x1}] - Coordinate System: In the Cartesian coordinate system, points are defined by pairs ((x, y)). The x-axis represents the horizontal direction, while the y-axis represents the vertical direction.
Method 1: Finding the Slope
Step 1: Find Two Different Points That the Line Passes Through
To calculate the slope, you must identify two distinct points on the line. These points can be obtained from a graph or as part of a problem. For example, let’s use points ((2, 3)) and ((5, 7)).
Step 2: Choose One Point as ((x1, y1)) and the Other as ((x2, y2))
Label the coordinates of the points to use them in the slope formula. For our example:
- Let ((x1, y1) = (2, 3))
- Let ((x2, y2) = (5, 7))
Step 3: Calculate (m) by Dividing the Rise by the Run
Use the slope formula to find the slope (m):
[m = \frac{y2 – y1}{x2 – x1}]
Substitute the values:
[m = \frac{7 – 3}{5 – 2} = \frac{4}{3}]
So, the slope of the line passing through the points ((2, 3)) and ((5, 7)) is (\frac{4}{3}).
Method 2: Types of Slopes
Understanding the different types of slopes is essential for interpreting the behavior of lines on a graph. Here are the four main types of slopes:
1. Positive Slope
- Definition: A line has a positive slope when it rises from left to right.
- Characteristics: Both the rise and the run are positive. The line angles upward.
- Example: A line passing through points ((1, 2)) and ((3, 5)) has a positive slope since it goes up as it moves from left to right.
Visual Representation
Imagine a hill you are climbing. As you move forward (right on the x-axis), you also move upward (up on the y-axis). This upward movement indicates a positive slope.
Calculation
For a positive slope, the formula (\frac{y2 – y1}{x2 – x1}) results in a positive number, indicating an upward trend.
2. Negative Slope
- Definition: A line has a negative slope when it falls from left to right.
- Characteristics: The rise is negative, and the run is positive. The line angles downward.
- Example: A line passing through points ((1, 5)) and ((3, 2)) has a negative slope since it goes down as it moves from left to right.
Visual Representation
Think of a ski slope. As you move forward (right on the x-axis), you move downward (down on the y-axis). This downward movement signifies a negative slope.
Calculation
For a negative slope, the formula (\frac{y2 – y1}{x2 – x1}) results in a negative number, indicating a downward trend.
3. Zero Slope
- Definition: A line has a zero slope when it is perfectly horizontal.
- Characteristics: The rise is zero, while the run is positive. There is no vertical change as you move along the line.
- Example: A line passing through points ((2, 3)) and ((5, 3)) has a zero slope since the y-coordinates are the same.
Visual Representation
Picture a flat road. No matter how far you travel forward (right on the x-axis), you do not move up or down (no change on the y-axis). This flat movement indicates a zero slope.
Calculation
For a zero slope, the formula (\frac{y_2 – y_1}{x_2 – x_1}) results in zero, indicating no vertical change.
4. Undefined Slope
- Definition: A line has an undefined slope when it is perfectly vertical.
- Characteristics: The run is zero, which makes the slope calculation involve division by zero, resulting in an undefined value.
- Example: A line passing through points ((4, 2)) and ((4, 5)) has an undefined slope since the x-coordinates are the same.
Visual Representation
Imagine a cliff. Moving vertically up or down without any horizontal movement (no change on the x-axis) indicates an undefined slope.
Calculation
For an undefined slope, the formula (\frac{y2 – y1}{x2 – x1}) involves division by zero, which is mathematically undefined.
Additional Tips for Calculating Slope
Graphical Method
Sometimes, visualizing the problem can help:
- Plotting Points: Plot the two points on a graph.
- Drawing the Line: Draw a straight line through the points.
- Counting Rise and Run: Count the units of rise (vertical change) and run (horizontal change) on the graph to calculate the slope.
Using Slope-Intercept Form
If you have the equation of a line in slope-intercept form ((y = mx + b)):
- Identify the Slope: The coefficient (m) is the slope of the line.
- Example: For the equation (y = 2x + 3), the slope (m) is 2.
Understanding Parallel and Perpendicular Slopes
- Parallel Lines: Parallel lines have the same slope. If line A has a slope of (m), then any line parallel to A also has a slope of (m).
- Perpendicular Lines: Perpendicular lines have slopes that are negative reciprocals of each other. If line A has a slope of (m), then a line perpendicular to A has a slope of (-\frac{1}{m}).
Practice Problems
Practicing with different sets of points can solidify your understanding:
- Problem 1: Find the slope of the line passing through points ((3, 4)) and ((6, 8)).
- Solution: (m = \frac{8 – 4}{6 – 3} = \frac{4}{3})
- Problem 2: Determine the slope of the line passing through points ((2, 5)) and ((2, 10)).
- Solution: The slope is undefined because the run is zero.
- Problem 3: Calculate the slope of the line passing through points ((7, 1)) and ((7, 1)).
- Solution: The slope is zero because the rise is zero.
Conclusion
Calculating the slope of a line is a fundamental skill in mathematics that helps in understanding the behavior of lines in a graph. By finding two points on the line, using the slope formula, and recognizing the type of slope, you can effectively determine the steepness and direction of any line. Whether the slope is positive, negative, zero, or undefined, each type provides valuable information about the line’s orientation and characteristics. By mastering these methods, you’ll be well-equipped to analyze and interpret linear relationships in various mathematical and real-world contexts.
Frequently Asked Questions:
- How do you calculate the slope of a line from a graph?
To calculate the slope of a line from a graph, follow these steps:
- Identify two distinct points on the line.
- Label these points as ((x_1, y_1)) and ((x_2, y_2)).
- Use the slope formula: (m = \frac{y_2 – y_1}{x_2 – x_1}).
- Substitute the coordinates of the points into the formula and simplify.
For example, if the points are ((2, 3)) and ((5, 7)), the slope is (m = \frac{7 – 3}{5 – 2} = \frac{4}{3}).
- What are the different types of slopes a line can have?
A line can have one of four types of slopes:
- Positive Slope: The line rises from left to right. Example: (m = \frac{4}{3}).
- Negative Slope: The line falls from left to right. Example: (m = -2).
- Zero Slope: The line is horizontal with no vertical change. Example: (m = 0).
- Undefined Slope: The line is vertical, making the run zero and the slope undefined. Example: division by zero.
- What does it mean if a line has a zero slope?
A line with a zero slope is perfectly horizontal. This means that for any two points on the line, the y-coordinates are the same, indicating no vertical change as you move along the line. In the slope formula (m = \frac{y_2 – y_1}{x_2 – x_1}), the numerator (rise) is zero, resulting in (m = 0). An example of such a line would be one passing through the points ((2, 3)) and ((5, 3)).
- How can you tell if two lines are parallel or perpendicular by their slopes?
To determine if two lines are parallel or perpendicular:
- Parallel Lines: Two lines are parallel if they have the same slope. For example, if line A has a slope of (m = 2) and line B also has a slope of (m = 2), they are parallel.
- Perpendicular Lines: Two lines are perpendicular if the product of their slopes is (-1). This means their slopes are negative reciprocals of each other. For example, if line A has a slope of (m = 2), then a line perpendicular to it will have a slope of (m = -\frac{1}{2}).
- How Does Automated Scheduling Save Time and Boost Engagement? - April 16, 2025
- 21 Delicious High Protein Foods - May 31, 2024
- Black Seed Oil: Health and Beauty Benefits - May 30, 2024